Non-linear optimization with constraints and extra arguments

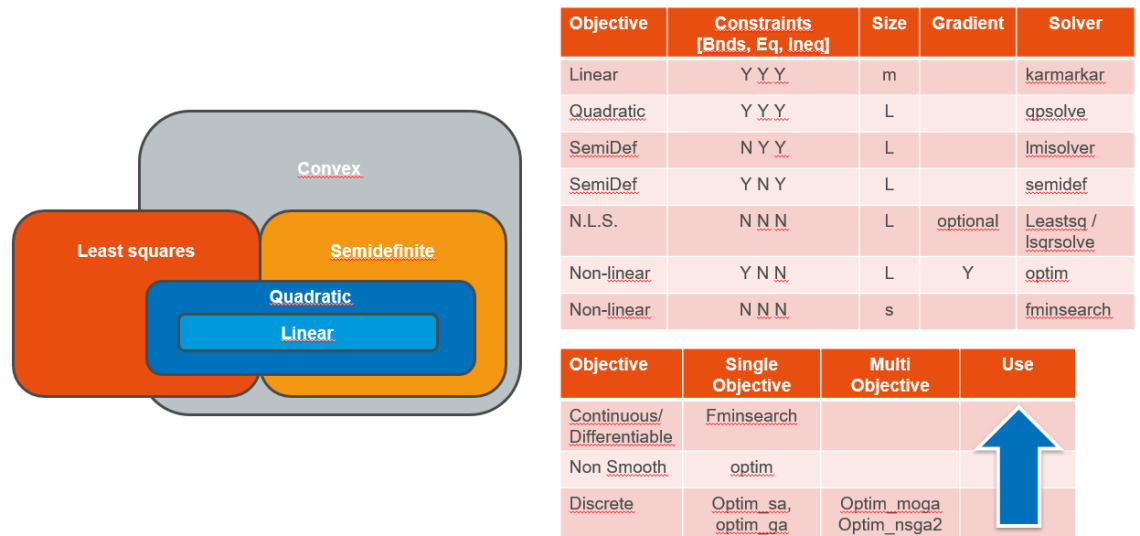
The content provided so far around optimization within SCILAB allowed you to solve different kind of problems: linear, quadratic, semi-definite, non-linear least squares, discrete, multiobjective, global ; leveraging differents techniques such as gradient methods, simplex, Genetic Algorithms and even Simulated Annealing. 

 

It is actually a set of pretty powerful capabilities I won't be focusing on in this tutorial. Instead, I will try to kill a myth which subsists since beginning of time ... Since SCILAB's beginning, actually, but trust me ... that's old!

SCILAB is actually providing tools to solve the most generic problem ever: Nonlinear optimization with constraints!

Isn't that epic? Well ... more that it sounds, actually. So let me show you what some people think isn't even possible.

For a deeper experience, you can download the script on top of this page.

The problem

For this tutorial, we will take the example of the Rosenbrock's Post Office problem which is stated as follow:

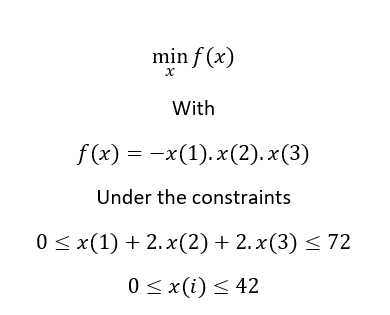
The extra argument trick

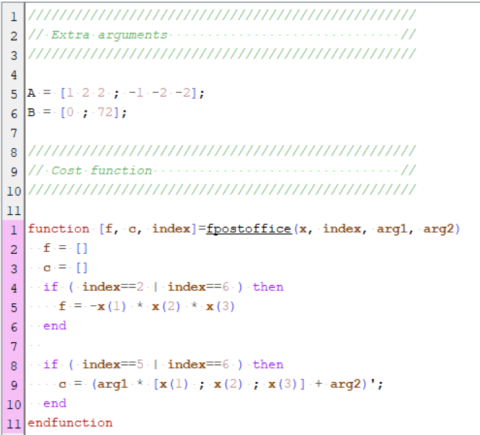
In this case, the objective function is pretty easy to set. To simplify the constraints, we will wrote them as a matrix inequality:

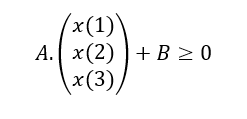
The associated Scilab code is as follow

 

In that case, we added some extra parameters to the cost function. To be honnest, that was not mandatory. We could obviously have hard coded the inequalities within the function. But in some cases, extra arguments computation is more complex or is coming from an imported file. In such cases, it is preferable to use this syntax rather than using global variables. Last step is then to use a list object to concatenate the cost function with the extra parameters you would like to use.

 

This trick can be used in pretty much every optimization function available within SCILAB.

The neldermead component

For this optimization we will use a simplex method. You might probably know the fminsearch function which is a packaged version of the simplex. This function is based on the neldermead component documented here.

The neldermead component is an object like structure created with the neldermead_new function. This object then needs to be configured before searching for optimal position using the neldermead_configure function. The optimization set up is similar to what is done for other optimization methods. Just make sure you selected the BOX method which allows you to implement constraints and specify the number inequality constraints using the nbineqconst parameter. The following code is therefore straightforward

 

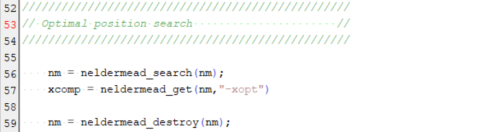
Finally you can run the optimization using the neldermead_search function and access the optimal position using the neldermead_get function with -xopt argument.

 

In xcomp we can then find the optimal solution minimizing our objective function which is (24, 12, 12).